逆解法与半逆解法

按应力函数求解

当体力为常量，按应力函数$\Phi$求解平面问题时，$\Phi $应满足：

$A$内相容方程${\nabla ^{\rm{4}}}\Phi {\rm{ = }0}$

$S = {S_\sigma }$上应力边界条件：

$$ \begin{array}{l} {(l{\sigma _x} + m{\tau _{yx}})_s} = \overline {{f_x}} \\ {(m{\sigma _y} + l{\tau _{xy}})_s} = \overline {{f_y}} \end{array} $$

逆解法

求解过程：

1. 先找出满足${\nabla ^{\rm{4}}}\Phi {\rm{ = }0}$的解$\Phi$;
2. 代入${\sigma _x} = \frac{{{\partial ^2}\Phi }}{{\partial {y^2}}} - {f_x}x,{\sigma _y} = \frac{{{\partial ^2}\Phi }}{{\partial {x^2}}} - {f_y}y,{\tau _{xy}} = - \frac{{{\partial ^2}\Phi }}{{\partial x\partial y}}$，求出应力分量
3. 在给定的边界形状$S$下，由应力边界条件方程反推出各边界上的面力
4. 最后得出在给定面力作用下的解答，就是上述$\Phi$和应力

半逆解法

求解过程：
1. 假设应力分量的函数形式（根据受力情况，边界条件等）
2. 由盈利函数形式，推测$\Phi$的函数形式
3. 代入${\nabla ^{\rm{4}}}\Phi {\rm{ = }0}$，解出$\Phi$
4. 由式子${\sigma _x} = \frac{{{\partial ^2}\Phi }}{{\partial {y^2}}} - {f_x}x,{\sigma _y} = \frac{{{\partial ^2}\Phi }}{{\partial {x^2}}} - {f_y}y,{\tau _{xy}} = - \frac{{{\partial ^2}\Phi }}{{\partial x\partial y}}$
5. 校核全部应力边界条件（对于多连体，还需满足位移单值条件）
6. 如满足为正确解答，否则修改假设。

例题

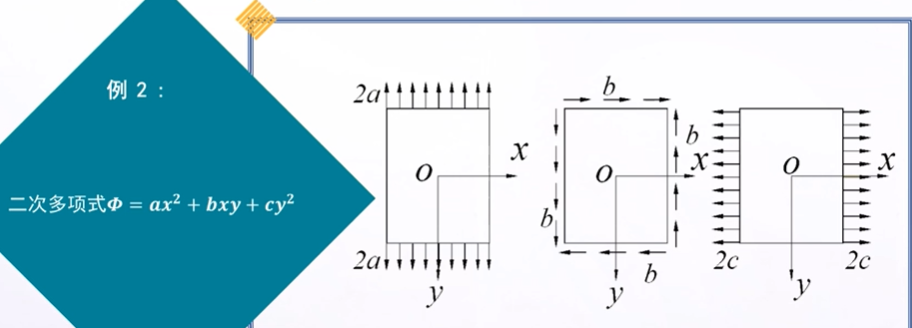
矩形梁的纯弯曲问题

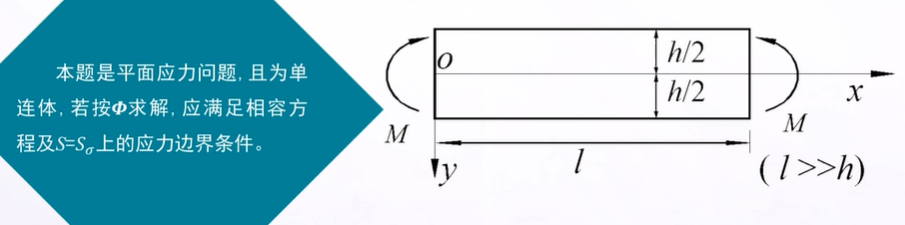
求解步骤：

1. 由逆解法得出。可取$\Phi = a{y^3}$，且满足${\nabla ^{\rm{4}}}\Phi {\rm{ = 0}}$
2. 求应力${\sigma _x} = 6ay,{\sigma _y} = {\tau _{xy}} = 0$
3. 检验应力边界条件：原则为
1. 先校核主要边界（大边界），必须精确满足应力边界条件
2. 再校核次要边界（小边界），若不能精确满足应力边界条件，则应用圣维南原理，用积分的应力边界条件代替
4. 解出主要边界的应力状态${\sigma _x} = \frac{{12M}}{{{h^3}}},{\sigma _y} = 0,{\tau _{xy}} = 0$与材料力学的，根据平截面假定推出的应力公式${\sigma _x} = \frac{{My}}{{{I_z}}}$是相同的。即平截面假定可能是精确的

位移分量的求出

提出问题：

在按应力求解中，若已得出应力，如何求出位移？

以纯弯曲问题为例，已知${\sigma _x} = \frac{{My}}{{{I_z}}},{\sigma _x} = {\tau _{xy}} = 0$试求解其位移。

解法：

先通过物理方程求应变：
$$ \begin{array}{l} {\varepsilon _x} = \frac{1}{E}({\sigma _x} - \mu {\sigma _y}) = \frac{M}{{EI}}y\\ {\varepsilon _y} = \frac{1}{E}({\sigma _y} - \mu {\sigma _x}) = - \frac{{\mu M}}{{EI}}y\\ {\gamma _{xy}} = \frac{{2(1 + \mu )}}{E}{\tau _{xy}} = 0 \end{array} $$

再代入几何方程求位移：
$$ \begin{array}{l} \frac{{\partial u}}{{\partial x}} = {\varepsilon _x} = \frac{M}{{EI}}y\\ \frac{{\partial v}}{{\partial y}} = {\varepsilon _y} = - \frac{{\mu M}}{{EI}}y\\ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = {\gamma _{xy}} = 0 \end{array} $$ $$ \begin{array}{l} u = \frac{M}{{EI}}xy + {f_1}(y)\\ v = - \frac{{\mu M}}{{EI}}{y^2} + {f_2}(x)\\ \frac{{Mx}}{{EI}} + \frac{{d{f_2}(x)}}{{dx}} = - \frac{{d{f_1}(y)}}{{dy}}( = \omega ) \end{array} $$

解出：

$$ \begin{array}{l} {f_1}(y) = - \omega y + {u_0}\\ {f_2}(x) = - \frac{M}{{2EI}}{x^2} + \omega x + {v_0} \end{array} =>\\ \begin{array}{l} u = \frac{M}{{EI}}xy - \omega y + {u_0}\\ v = - \frac{{\mu M}}{{2EI}}{y^2} - \frac{M}{{2EI}}{x^2} + \omega x + {v_0} \end{array} $$

由边界约束条件,确定刚体的位移分量$u,v,\omega $

弯应力${\sigma _x}$与材料力学的解相同

铅直线的转角$\beta = \frac{{\partial u}}{{\partial y}} = \frac{M}{{EI}}x - \omega $,故在任一截面$x$处,平截面假设成立

纵向纤维的曲率$\frac{1}{\rho } = - \frac{{{\partial ^2}v}}{{\partial {x^2}}} = \frac{M}{{EI}}$同材料力学的结果,故在纯弯曲情况下,弹性力学与材料力学的解相同。

简支梁受均布荷载

题目

简支梁$ {2lh1} $，受均布荷载$q$及两端支承反力$ql$

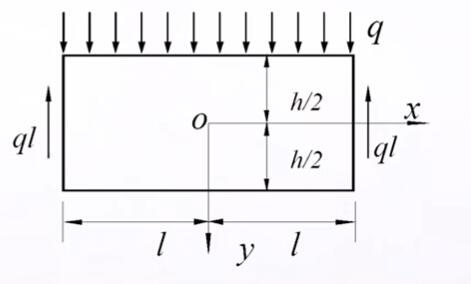
求解过程

假设应力分量

由材料力学${\sigma _x} \propto M,\tau \propto {F_s},{\sigma _y} \propto q$，因为${\sigma _y} \propto q$为常数,可假设${\sigma _y} = f(y)$

由应力分量推出应力函数

$\frac{{{\partial ^2}\Phi }}{{\partial {x^2}}} = {\sigma _y} = f(y)$ 对$x$积分，$\frac{{\partial \Phi }}{{\partial x}} = xf(y) + {f_1}(y)$ 对$x$再积分 $\Phi = \frac{{{x^2}}}{2}f(y) + x{f_1}(y) + {f_2}(y)$

将$\Phi $代入相容方程，$\Phi $

$$ \frac{1}{2}\frac{{{d^4}f(y)}}{{d{y^4}}}{x^2} + \frac{{{d^4}{f_1}(y)}}{{d{y^4}}}x + (\frac{{{d^4}{f_2}(y)}}{{d{y^4}}} + 2\frac{{{d^2}f(y)}}{{d{y^2}}}) = 0 $$

x的0，1，2次放的系数等于0

解出

$$ \left. \begin{array}{l} f = A{y^3} + B{y^2} + cy + D\\ {f_1} = E{y^3} + F{y^2} + Gy\\ {f_2} = - \frac{A}{{10}}{y^5} - \frac{B}{6}{y^4} + H{y^3} + K{y^2} \end{array} \right\} $$

由$\Phi $求应力

对称条件——由于结构和荷载对称于$y$轴,故$\Phi ,{\sigma _x},{\sigma _y}$应为x的偶函数，${\tau _{xy}}$为x的奇函数，故$E=F=G=0$

考察边界条件

1. 每个边界都要满足相应的边界条件
2. 复核过程中，求得待定系数

$$ 主要边界：(y = \pm \frac{h}{2})\\ \begin{array}{l} {({\sigma _y})_{y = h/2}} = 0,\\ {({\sigma _y})_{y = - h/2}} = - q,\\ {({\tau _{xy}})_{y = \pm h/2}} = 0 \end{array} $$ 解出系数A、B、C、D 对于次要边界（$x=l$），应用圣维南原理的积分条件解出H、K 得到应力解答： $$ \begin{array}{l} {\sigma _x} = \frac{{6q}}{{{h^3}}}({l^2} - {x^2})y + q\frac{y}{h}(4\frac{{{y^2}}}{{{h^2}}} - \frac{3}{5})\\ = \frac{M}{l}y + q\frac{y}{h}(4\frac{{{y^2}}}{{{h^2}}} - \frac{3}{5})\\ {\tau _{xy}} = \frac{{6q}}{{{h^3}}}x(\frac{{{h^2}}}{{\rm{4}}} - {y^2}) = \frac{{{F_s}S}}{{bl}}\\ {\sigma _y} = - \frac{q}{2}(1 - \frac{y}{h}){(1 - \frac{{2y}}{h})^2} \end{array} $$

弹性力学解与材料力学解

x方向的正应力第一项与$q{(\frac{l}{h})^2}$同阶，与材料力学解相同
第二项与$q$同阶（弹性力学的修正项）
x面上y方向上的切应力与$q{(\frac{l}{h})^2}$同阶，与材料力学解相同
y方向上的正应力与$q$同阶，材料力学不计。

锲形体受重力及液体压力

题目

设有锲形体,左面垂直,顶角为$\alpha$,下端无限长,受重力及齐顶液体压力$ {f_x}=0, {f_y} = {{\rho _1}}g\$

求解-量纲分析法

假设应力

因为应力$ \propto {\rho _{\rm{1}}}g,{\rho _2}g$,而应力的量纲只比${\rho _{\rm{1}}}g,{\rho _2}g$高一次.
所以应力$=({\rho _{\rm{1}}}g,{\rho _2}g) \times (x,y一次式)$
即可假设应力 为x,y的一次式

得应力函数关系式

$\Phi {\rm{ = }}a{x^3} + b{x^2}y + cx{y^2} + d{y^3}$ 满足相容方程: ${\nabla ^4}\Phi = 0$

求解应力

$$ \begin{array}{l} {\sigma _x} = \frac{{{\partial ^2}\Phi }}{{\partial {y^2}}} - {f_x}x = 2cx + 6dy\\ {\sigma _x} = \frac{{{\partial ^2}\Phi }}{{\partial {x^2}}} - {f_y}y = 6ax + 2by - {\rho _1}gy\\ {\tau _{xy}} = - \frac{{{\partial ^2}\Phi }}{{\partial x\partial y}} = - 2bx - 2cy \end{array} $$

考察边界条件

本题两个大边界,应力边界条件必须严格满足应力边界条件

$x=0$ 铅直面

${({\sigma _x})_{x = 0}} = - {\rho _2}gy$,解出$d = \frac{{{\rho _2}g}}{6}$ ${({\tau _{xy}})_{x = 0}} = 0$,解出$c=0$ $x=y{\tan \alpha}$ 斜边界 $$ \begin{array}{l} {\sigma _x} = - {\rho _2}gy\\ {\sigma _y} = ({\rho _1}gy\cot \alpha - 2{\rho _2}g{\cot ^3}\alpha )x\\ + ({\rho _2}g{\cot ^2}\alpha - {\rho _1}g)y\\ {\tau _{xy}} = - {\rho _2}gx{\cot ^2}\alpha \end{array} $$

解答的应用

1. 作为重力的解答参考-坝体中部的应力,接近锲形体的解答
2. 重力坝规范规定的解法-材料力学解法
3. 重力坝的精确分析,可按有限单元法进行